 Redis数据结构(一)Hyperloglog的实现原理
Redis数据结构(一)Hyperloglog的实现原理
# Redis数据结构(一)hyperloglog的实现原理
# 一、前言
# 1、介绍
介绍hyperloglog之前,我们先认识一下伯努利试验(Bernoulli experiment),伯努利试验是在同样的条件下重复地、相互独立地进行的一种随机试验,其特点是该随机试验只有两种可能结果:发生或者不发生。我们假设该项试验独立重复地进行了n次,那么就称这一系列重复独立的随机试验为n重伯努利试验,或称为伯努利概型
# 2、推论
设在一次试验中,事件A首次发生的概率为p(0<p<1),则在伯努利试验序列中,事件A在第 k 次试验中才首次发生的概率为: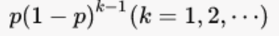
# 3、示例
在一个抛硬币的场景下,假设硬币的正面对应着 1,硬币的反面对应着0, 依次扔出 0,0,0,1 的概率是多少?通过概率计算可以得到是这个概率是 1/16,那么相当于平均需要扔 16次,才会获得 0,0,0,1 这个序列。反之,如果出现了 0,0,0,1 这个序列,说明起码抛了 16 次硬币, 也就是说:
- 出现序列 01XXXX意味着不重复的元素估计有 4 个;
- 出现序列 001XXX 意味着不重复的元素估计有 8个;
- 出现序列 0001XX意味着不重复的元素估计有 16 个;
- 出现序列 00001X意味着不重复的元素估计有 32个;
HyperLogLog 是一种基数估算算法。所谓基数估算,就是估算在一批数据中,不重复元素的个数有多少。最常见的场景就是统计uv。 首先要说明,HyperLogLog实际上不会存储每个元素的值,它使用的是概率算法,通过存储元素的hash值的第一个1的位置,来计算元素数量。这样做存在误差,不适合绝对准确计数的场景。
# 二、hyperloglog底层结构分析
# 1、存储结构
struct hllhdr {
char magic[4]; /*魔法值 "HYLL" */
uint8_t encoding; /* 密集结构或者稀疏结构 HLL_DENSE or HLL_SPARSE. */
uint8_t notused[3]; /*保留位, 全为0. Reserved for future use, must be zero. */
uint8_t card[8]; /* 基数大小的缓存 Cached cardinality, little endian. */
uint8_t registers[]; /* 数据字节数组Data bytes. */
};
2
3
4
5
6
7
# 2、结构划分
# 密集存储结构
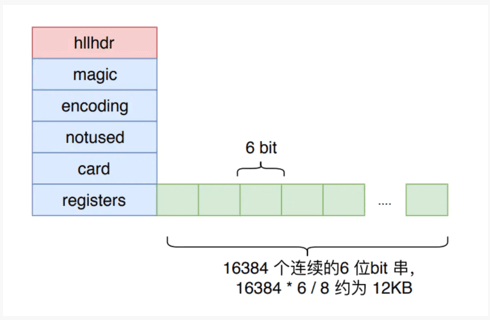
# 稀疏存储结构
HyperLogLog 的稀疏存储结构是为了节约内存消耗,它不像密集存储模式一样,真正找了那么多个字节数组来表示2^14 个桶,而是使用特殊的字节结构来表达
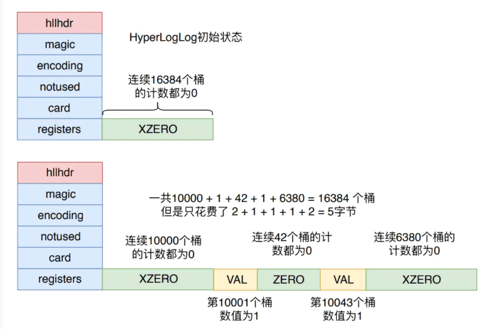
Redis 为了方便表达稀疏存储,它将上面三种字节表示形式分别赋予了一条指令
- ZERO : 一字节,表示连续多少个桶计数为0,前两位为标志00,后6位表示有多少个桶,最大为64。
- XZERO : 两个字节,表示连续多少个桶计数为0,前两位为标志01,后14位表示有多少个桶,最大为16384
- VAL : 一字节,表示连续多少个桶的计数为多少,前一位为标志1,四位表示连桶内计数,所以最大表示桶的计数为32。后两位表示连续多少个桶
稀疏存储转换到密集存储
1>任意一个计数值从 32 变成 33,因为 VAL 指令已经无法容纳,它能表示的计数值最大为 32
2>稀疏存储占用的总字节数超过 3000 字节,这个阈值可以通过 hll_sparse_max_bytes 参数进行调整
# 三、hyperloglog过程
redis在接收到字符串的时候,会就行hash运算,得到64位比特串

HyperLogLog 将上文所说的 64 位比特串的低 14 位单独拿出,它的值就对应桶的序号,然后将剩下 50 位中第一次出现 1 的位置 值设置到桶中。50位中出现1的位置值最大为50,所以每个桶中的 6 位数组正好可以表示该值。
在设置前,要设置进桶的值是否大于桶中的旧值,如果大于才进行设置,否则不进行设置。

使用上面给出的
DV公式根据桶中的数值,计算基数。此处公式不做展示,可参考文献 (opens new window)
# 四、Demo在线演示地址
http://content.research.neustar.biz/blog/hll.html (opens new window)
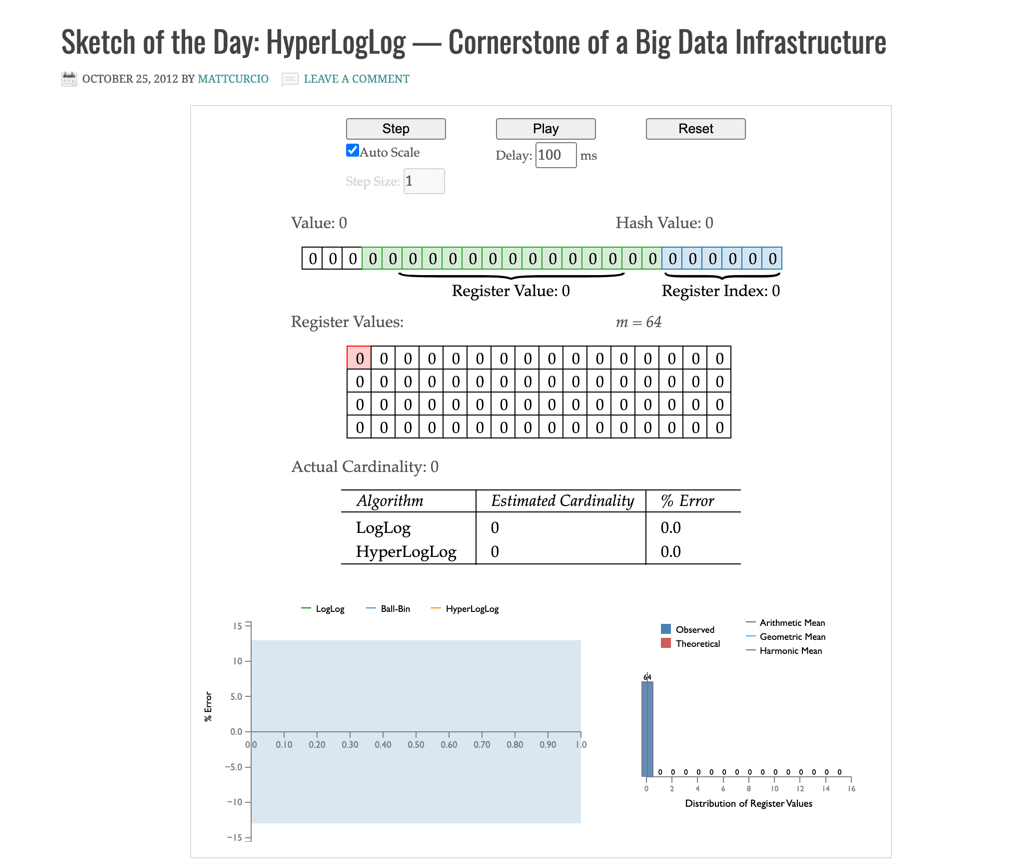
# 五、常用命令
下表列出了 redis HyperLogLog 的基本命令
| 序号 | 命令及描述 |
|---|---|
| 1 | [PFADD key element element ...] 添加指定元素到 HyperLogLog 中。 |
| 2 | [PFCOUNT key key ...] 返回给定 HyperLogLog 的基数估算值。 |
| 3 | [PFMERGE destkey sourcekey sourcekey ...] 将多个 HyperLogLog 合并为一个 HyperLogLog |
# 六、应用场景
Redis HyperLogLog 是用来做基数统计的算法,例如:页面UV
对于上面的场景,可以使用HashMap、BitMap和HyperLogLog来解决。对于这三种解决方案,这边做下对比
HashMap:算法简单,统计精度高,对于少量数据建议使用,但是对于大量的数据会占用很大内存空间;
BitMap:位图算法,具体内容可以参考我的这篇文章,统计精度高,虽然内存占用要比HashMap少,
但是对于大量数据还是会占用较大内存;
HyperLogLog:redis中实现的HyperLogLog,只需要12K内存,在标准误差低于1%的前提下,能够统计2^64个数据
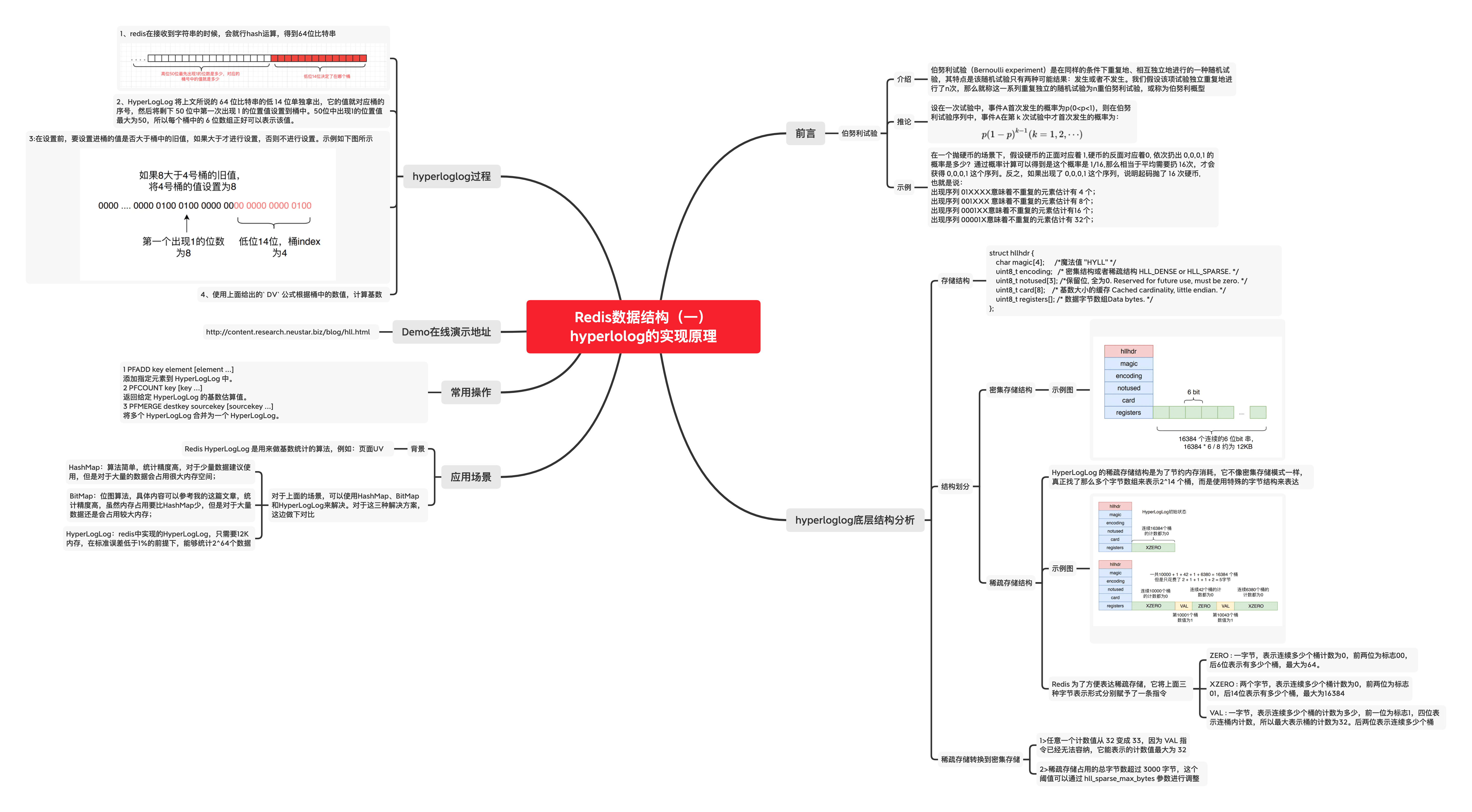
# 七、思维导图
# 八、参考文档
HyperLogLog: the analysis of a near-optimal cardinality estimation algorithm (opens new window)
